
TIGRO
TIGRO 1: Addition und Subtraktion
TIGRO 1: Addition und Subtraktion
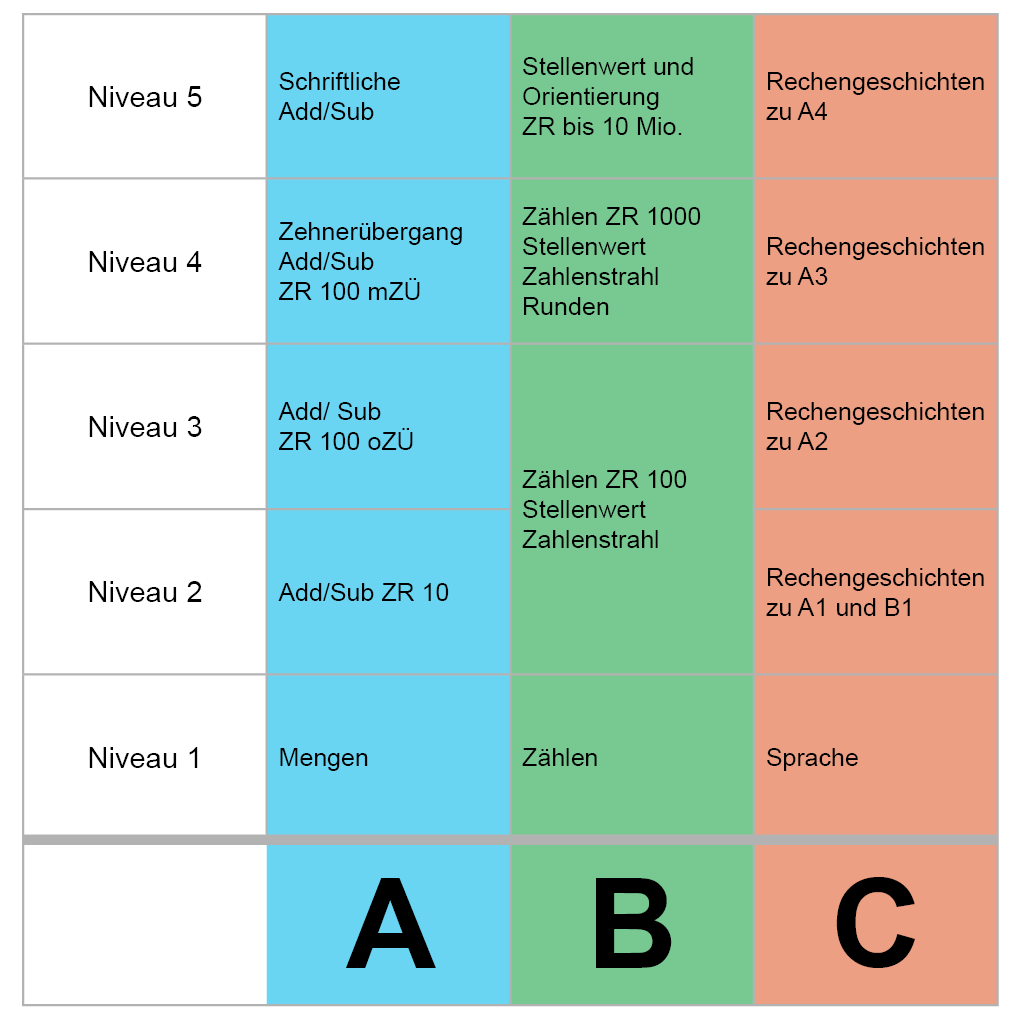
TIGRO 1 widmet sich den Operationen Addition und Subtraktion. Der modular-hierarchische Aufbau in 3 Säulen (Mengen, Zählen, Sprache) und 5 Niveaus unterstützt Individualisierung und Differenzierung und ermöglicht die optimale Anpassung an den jeweiligen Lernstand.
Modular-hierarchischer Aufbau
Das Programm ist sowohl in Niveaus als auch in Säulen unterteilt. Nach dem Triple-Code-Modell (Dehaene, 1992) ist es unumstritten, dass Teilkompetenzen im mathematischen Bereich nicht nur hierarchisch, sondern auch modular aufgebaut sind. Bestimmte arithmetische Teilfertigkeiten können also mehr oder weniger beeinträchtigt sein als andere.
Mit TIGRO ist es möglich, die jeweiligen Säulen auf verschiedenen Niveaus zu bearbeiten und genau dort anzusetzen, wo das Kind noch Lücken hat.
TIGRO 1 - Addition und Subtraktion
Jede der drei Säulen Mengen, Zählen und Sprache wird Schritt für Schritt aufgebaut. Zum nächsten Niveau wird erst übergegangen, wenn das vorangegangene gesichert ist.
So werden in Säule A vor den ersten Rechenaufgaben zuerst die Mengenvorstellung überprüft. Hierzu gibt es verschiedene Zähl- und Abschätzaufgaben zum Erfassen von Mengen (z.B. „Blitzmengen“). Das Vergleichen von Mengen wird eingeübt, es werden verschiedene Mengenrepräsentationen automatisiert (Würfelbild, Fingerbild), Mengen sortiert und in Teilmengen zerlegt. Erst wenn all diese Fähigkeiten aufgebaut und automatisiert sind, wird zu ersten Rechnungen übergegangen.
Ebenso wird vor dem Bearbeiten von Textaufgaben zuerst die mathematische Sprache aufgebaut, der Unterschied zwischen Kardinal- und Ordinalzahlen (Zeige mir das dritte Haus oder drei Häuser.), Begriffe wie mehr, weniger, einige, keine, alle, beide, … geklärt und eingeübt, die Lesefertigkeiten überprüft und weitere mathematische Begriffe durch Spiele und Übungen gesichert (halb so viel, doppelt so viel, Unterschied, Ergebnis, etwas wegnehmen, …). Die Rechnungen bei den Textaufgaben orientieren sich immer an einem niedrigeren Niveau, um sicherzustellen, dass die Aufgaben rechnerisch gelöst werden können. (Auf Niveau 2 behandeln die Rechengeschichten Aufgaben zu Mengen und zum Zählen aus Niveau 1.)
Das kleinschrittige Vorgehen hilft beim Sichern aller notwendigen Grundlagen. Das Arbeiten an der Null-Fehler-Grenze ermöglicht das kontinuierliche Aufbauen von tragfähigem mathematischem Vorwissen, kurz: Es wird die Basis für konsistente, dauerhafte Lernerfolge geschaffen.
Blick ins Material
Mengen, Zählen, Sprache
Die drei Säulen Menge, Zählen und Sprache bilden die Basis von TIGRO 1. Säule A befasst sich mit Mengen, Fakten und Prozeduren. Bei Säule B stehen das Zählen, die Orientierung im Zahlenraum, das Stellenwertverständnis und der Zahlenstrahl im Fokus. Die dritte Säule C befasst sich mit dem Aufbau der mathematischen Sprache, also dem Kennenlernen von einschlägigen Begriffen (mehr, weniger, nichts, Nachfolger, Vorgänger, Ergebnis …), und bereitet Sachrechnungen bzw. Textaufgaben in kleinen Schritten vor.
Da Sachrechnungen auch Kindern ohne Rechenschwäche häufig Schwierigkeiten bereiten, gibt TIGRO diesem Bereich mit kleinschrittigen Einführungen ausreichend Raum.
Inhalt
A.1
B.1
C.1
A.2
B.2
C.2
A.3
C.3
A.4
B.4
C.4
A.5
B.5
C.5